Seno, cosseno e tangente são elementos da trigonometria, um ramo da matemática que estuda a relação entre comprimentos e ângulos nos triângulos.
Apesar de relacionarem muito o seno, cosseno e tangente somente com os triângulos retângulos, essas relações existem em qualquer triângulo.
Índice
- Fórmula do seno, cosseno e tangente
- Triângulo retângulo
- Seno
- Cosseno
- Tangente
- Ângulos notáveis
- Vídeo aula com exercícios
- Material complementar
FÓRMULA DO SENO, COSSENO E TANGENTE
Um resumão das fórmulas para quem está procurando somente pelas fórmulas:

TRIÂNGULO RETÂNGULO
Triângulo retângulo é caracterizado por possuir um ângulo de 90°, dois catetos e uma hipotenusa. Assim como todos os triângulos, a soma dos ângulos internos é igual a 180°. A imagem abaixo representa um triângulo retângulo.
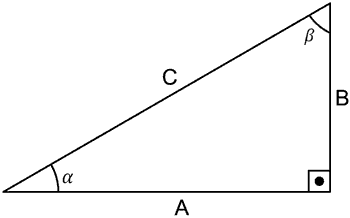
- Catetos: A e B
- Hipotenusa: C
Ademais, conhecer o Teorema de Pitágoras pode ajudar a resolver diversos exercícios sobre relações trigonométricas.
CATETO OPOSTO
O cateto oposto fica do lado oposto ao ângulo de referência. No triângulo acima temos a seguinte situação:
- Lado A é cateto oposto ao ângulo β
- Lado B é cateto oposto ao ângulo α
CATETO ADJACENTE
O cateto adjacente fica adjacente, ou seja, junto ao ângulo de referência. No triângulo acima temos a seguinte situação:
- Lado A é cateto adjacente ao ângulo α
- Lado B é cateto oposto ao ângulo β
HIPOTENUSA
A hipotenusa é o maior lado no triângulo retângulo. Pelo Teorema de Pitágoras, podemos estabelecer a fórmula da hipotenusa:
- O quadrado da hipotenusa é igual à soma do quadrado dos catetos
C² = A² + B²
SENO
Seno é o quociente da razão entre o cateto oposto e a hipotenusa. Dessa forma, dada a imagem abaixo, podemos dizer que o seno do ângulo α é a razão da altura do prédio pela hipotenusa.

FÓRMULA DO SENO
Dito isso, podemos escrever a fórmula do seno no triângulo retângulo:
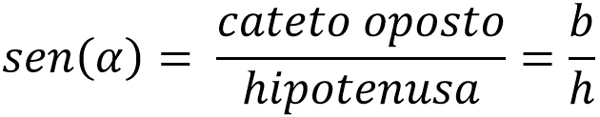
LEI DOS SENOS
Além disso, temos a Lei dos Senos que estabelece uma relação entre todos os senos e lados de qualquer triângulo.
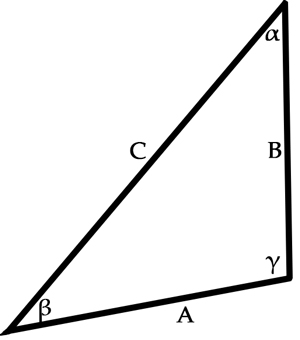
Assim, pela Lei dos Senos temos a seguinte fórmula:
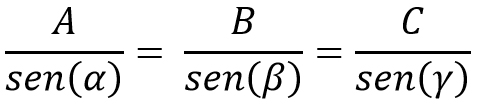
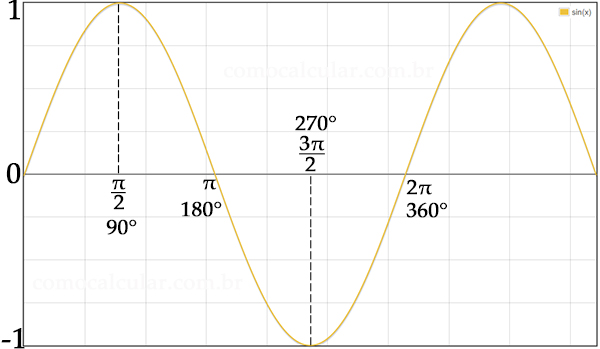
GRÁFICO DO SENO
O seno pode ser representado em gráfico pelo movimento ondulatório periódico com amplitude entre -1 e +1, sendo que o ponto inicial é no ponto (0,0).
COSSENO
Cosseno é o quociente da razão entre o cateto adjacente e a hipotenusa. Dessa forma, dada a imagem abaixo, podemos dizer que o cosseno do ângulo α é a razão da distância até o prédio e a hipotenusa.

FÓRMULA DO COSSENO
Dito isso, podemos escrever a fórmula do cosseno no triângulo retângulo:

LEI DOS COSSENOS
Além disso, temos a Lei dos Cossenos que estabelece uma relação entre todos os lados e o cosseno de qualquer triângulo.

Assim, pela Lei dos Cossenos temos a seguinte fórmula:

GRÁFICO DO COSSENO
O cosseno pode ser representado em gráfico pelo movimento ondulatório periódico com amplitude entre -1 e +1, sendo que o ponto inicial é no ponto (0,1).

TANGENTE
Tangente é o quociente da razão entre o cateto oposto e o cateto adjacente. Além disso, vinculamos outra fórmula à tangente, mas que na verdade é apenas um rearranjo da fórmula anterior. Assim, dizemos que a tangente é igual ao quociente da razão entre o seno e cosseno. Dessa forma, dada a imagem abaixo, podemos dizer que a tangente do ângulo α é a razão da altura pela distância até o prédio.

FÓRMULA DA TANGENTE
Dito isso, podemos escrever a fórmula da tangente no triângulo retângulo:
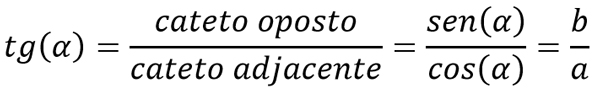
GRÁFICO DA TANGENTE
A tangente pode ser representado em gráfico pelo movimento periódico com amplitude infinita, sendo que o ponto inicial é no ponto (0,0).

Na contramão dos gráficos do seno e cosseno, o gráfico da tangente é inexistente nos ângulos 90°, 270° e assim sucessivamente.
ÂNGULOS NOTÁVEIS
Os ângulos de 30°, 45° e 60° são considerados notáveis. É importante saber o seno, cosseno e a tangente desses ângulos, pois são bastante utilizados nos exercícios. Veja a tabela do seno, cosseno e tangente dos ângulos notáveis.

Gostei
gostei,boa explição
Eu gostei muito
Muito boas as explicações…
Informação sobre o curso de matemática por favor.