Índice
- O que são juros compostos?
- Fórmula dos juros compostos
- Como calcular juros compostos
- Diferença entre juros simples e compostos
- Gráfico
- Exercícios resolvidos
O QUE SÃO JUROS COMPOSTOS?
Juros compostos são valores resultantes da aplicação de um capital por um determinado período de tempo a uma taxa. Porém, diferente do juros simples, os juros compostos são acrescentados ao capital. Por isso, o crescimento dos juros compostos se dá de forma exponencial.
FÓRMULA DOS JUROS COMPOSTOS
A fórmula dos juros compostos é o produto do capital com a soma de 1 mais a taxa elevada ao tempo de aplicação.
Além disso, tem a fórmula geral do montante, que é a soma do capital e juros e pode ser utilizada tanto nos juros simples quanto nos juros compostos.
O tempo é um expoente, por isso os juros compostos crescem exponencialmente conforme o tempo de aplicação do capital.
COMO CALCULAR JUROS COMPOSTOS
Para calcular os juros compostos, siga o passo a passo:
- Leia o exercício
- Entenda o que está sendo pedido
- Extraia os dados que compõem a fórmula: montante, capital, taxa e tempo. Geralmente um desses não será informado
- Substitua os dados na fórmula
JUROS COMPOSTOS NO EXCEL
Para calcular juros compostos no Excel, como na imagem acima, utilize as seguintes fórmulas nas células E2 e D2, respectivamente.
=A2*(1+B2)^C2
=E2-A2JUROS COMPOSTOS NA HP 12C
Para calcular juros compostos na calculadora HP 12C siga os passos abaixo:
- Digite o capital inicial, aperte CHS e depois PV
- Digite a taxa de juros e aperte i
- Digite o tempo e aperte n
- Aperte FV. Esse é o montante.
- Digite o capital inicial e aperte -. Esse é o juros.
COMO CALCULAR A TAXA DE JUROS COMPOSTOS NA HP 12C
Para calcular a taxa de juros compostos na HP 12, siga os passos abaixo:
- Digite o capital inicial, aperte CHS e depois PV
- Digite o tempo e aperte n
- Digite o montante e aperte FV
- Digite i. Essa é a taxa.
DIFERENÇA ENTRE JUROS SIMPLES E COMPOSTOS
A diferença é que em juros simples a taxa incide somente sobre o capital inicial, que é constante, por outro lado, nos juros compostos a taxa incide sobre o capital inicial somado aos juros.
Preparei uma tabela no Excel para visualizar a diferença entre juros simples e juros compostos.
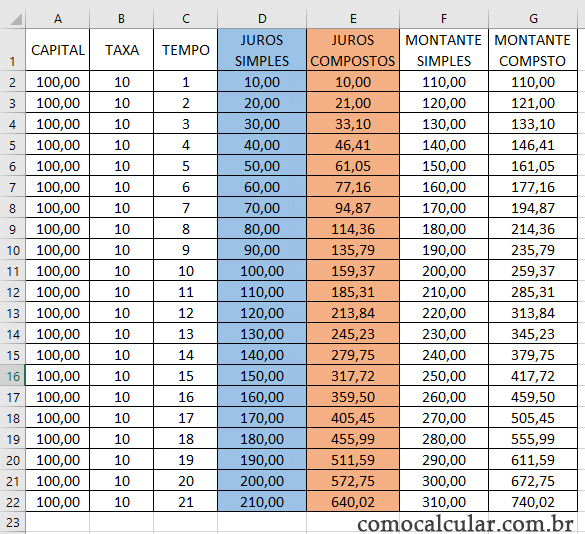
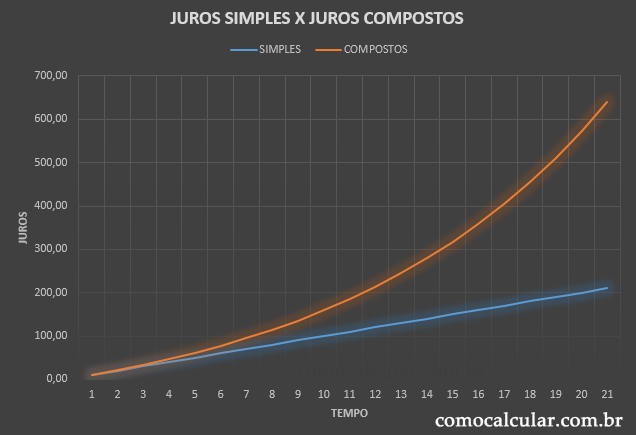
Dessa forma, o poder do juros compostos está no fato dele crescer exponencialmente, enquanto o juros simples cresce linearmente.
GRÁFICO
Ademais, preparei um gráfico comparativo no Excel entre juros simples e juros compostos.
EXERCÍCIOS RESOLVIDOS
1 – Considere R$1.000,00 aplicado a uma taxa de 2%a.m durante 3 meses. Qual o montante ao final desse período?
Esse é um exercício considerado fácil, pois todos as variáveis que compõem a fórmula já estão informadas no enunciado.
- Capital (C) = 1.000
- Taxa (i) = 2%a.m
- Prazo (n) = 3 meses
Agora que os dados estão organizados, vamos colocar na fórmula.
Portanto, ao final dos 3 meses de aplicação vamos resgatar R$1.061,20, portanto os juros sobre o capital aplicado foi de R$61,20.
Aposentadoria é um bom negócio?
Homens – 35 anos de contribuição.
Teto máximo…
Para facilitar os cálculos..
Aporte mensal 1.000.00 por 35 anos = 420 contribuições.
Depois de aposentado, a renda seria de 5.000.00 mensais.
O montante final daria para pagar quantos salários de aposentadoria a 5.000.00 mensais, considerando juros de 0.5% mensais….
assim
2000,00 menos a entrada de 400,00 vai parcelar apenas 1600,00 ok
1600 4 64,oo 1664,00
1664 4 66,56 1730,56
1730,56 4 6922 1799,78
3 parcelas de 599,92
2- Os juros reais das caderneta de poupança são de 6% a.a,, Com capitalização mensais… Qual a taxa efetiva ao ano
A taxa 6% a.a. é a taxa nominal. 6% ao ano com capitalização mensal, a taxa refere-se a períodos diferentes. Primeiro encontramos a taxa efetiva mensal a 6% a.a. Basta dividir 6/12 (um ano= 12 meses), que da 0,5% a.m. Depois calculamos a taxa equivalente a 0,5% a.m ao ano. Existem algumas formulas para isso. Pessoalmente prefiro esta: (1+iM) = (1+im)^n, onde iM = taxa do período maior, im = taxa do período menor e n é o período. Assim temos:
(1+iM)= (1+ 0,005)^12
resolvendo
1+ iM = 1,005^12
1+iM = 1,061677812
iM= 0.061677812 ou 6,16% a.a. (taxa efetiva ao ano)
Na HP12
100 CHS PV
12 n
0,5 i
FV
100-
6,167% a.a.
Poderia me ajudar nesses dois casos.
1) Um bem Vale R$ 2.000,00 Á Vista, A Prazo , paga-se uma entrada de 20% mais 03 parcelas iguais e consecutivas. A juros compostos de 4% a.m,, Calcular o Valor das Mensalidades.
2) Os juros reais das caderneta de poupança são de 6% a.a,, Com capitalização mensais… Qual a taxa efetiva ao ano
3)Uma Pessoa compra um equipamento que irá pagar em 5 prestações mensais de R$ 2.600,00 sem entrada, com taxas de juros compostos 2% a.m. Qual o Preço à vista;…
Já tentei por varias vezes fazer esses três mas não consegui resultado satisfatório, já usei a formula do montante, mas sem chance,,, se puder me ajudar com a formula e resolução eu ficaria bastante grato
2- Os juros reais das caderneta de poupança são de 6% a.a,, Com capitalização mensais… Qual a taxa efetiva ao ano
A taxa 6% a.a. é a taxa nominal. 6% ao ano com capitalização mensal, a taxa refere-se a períodos diferentes. Primeiro encontramos a taxa efetiva mensal a 6% a.a. Basta dividir 6/12 (um ano= 12 meses), que da 0,5% a.m. Depois calculamos a taxa equivalente a 0,5% a.m ao ano. Existem algumas formulas para isso. Pessoalmente prefiro esta: (1+iM) = (1+im)^n, onde iM = taxa do período maior, im = taxa do período menor e n é o período. Assim temos:
(1+iM)= (1+ 0,005)^12
resolvendo
1+ iM = 1,005^12
1+iM = 1,061677812
iM= 0.061677812 ou 6,16% a.a. (taxa efetiva ao ano)
Na HP12
100 CHS PV
12 n
0,5 i
FV
100-
6,167% a.a.
R= 1600*0,04*(1*040^3/(1.04)^3-1=576,56