Regra de três é uma técnica matemática utilizada para calcular uma incógnita quando conhecemos pelo menos três valores das duas ou mais grandezas.
Exercícios Resolvidos
1 – Determine se as grandezas são diretamente ou inversamente proporcionais.
a) Quantidade de trabalhadores e a produção diária de peças.
“Quanto maior/mais o(a)________ maior/menor/mais/menos será o(a)____________.”
b) Hora diária de trabalho e a quantidade de trabalhadores.
c) Vazão de água de uma represa e o nível de água na represa.
d) Quantidade de alimentos em estoque e o tempo que será possível alimentar 4 pessoas antes de repor o estoque.
e) Quantidade de vacas e a produção diária de leite.
f) Velocidade do veículo e o tempo para percorrer determinado percurso.
g) Eficiência dos pedreiros e tempo da obra.
h) Hora diária de trabalho e a rapidez para terminar certo trabalho.
2 – Uma obra deveria ser concluída em 20 dias e para isso foram contratados 4 trabalhadores. Se o prazo fosse de 15 dias, quantos trabalhadores, no mínimo, teriam de ser contratados?
O primeiro passo é identificar as grandezas: dias e trabalhadores. O segundo passo é identificar se as grandezas são diretamente ou inversamente proporcionais entre si. O terceiro passo é identificar os valores vinculados às grandezas e montar a regra de três.

No mínimo 6, pois se contratar só 5 não será o suficiente e não é possível contratar 5,33 homens.
3 – Uma família de 5 pessoas estocou 50Kg de alimentos que são suficientes para alimenta-los durante 5 dias. Por quantos dias será possível alimentar uma família com 7 pessoas com 70 Kg de alimentos estocados?
Esse exercício de regra de três é típico de concurso público, pois a resposta mais óbvia seria 7, só que não. Vamos seguir o passo a passo para resolver regra de três. Podemos verificar que esse exercício trata de uma regra de três composta, pois possui mais de duas grandezas.
- Identificar as grandezas: pessoas, alimentos e dias.
- Identificar se as grandezas são diretamente ou inversamente proporcionais em relação à grandeza com a incógnita.
- Identificar os valores vinculados às grandezas e montar a regra de três.

4 – Um trabalho foi executado por 30 pessoas com eficiência de 60% em 45 dias trabalhando 8 horas por dia. Quantas pessoas seriam necessárias para terminar o trabalho em 30 dias, trabalhando 6 horas por dia com 100% de eficiência?
Esse exercício envolve quatro grandezas, portanto a organização torna-se ainda mais importante para não misturar nada. Os exercícios de regra de três são resolvidos sempre do mesmo modo, portanto vamos seguir o passo a passo.
- Identificar as grandezas: pessoas, eficiência, dias e horas/dia.
- Identificar se as grandezas são diretamente ou inversamente proporcionais em relação à grandeza com a incógnita.
- Identificar os valores vinculados às grandezas e montar a regra de três.
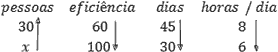
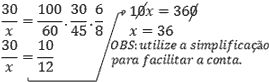
5 – Em uma indústria são utilizadas 15 máquinas novas com 95% de eficiência. Nessas condições, as máquinas produzem 800 peças, funcionando 18 horas por dia. Após alguns anos, foram adquiridas 5 máquinas novas e a eficiência geral diminuiu para 75% devido ao desgaste das demais máquinas. Sabendo que agora as máquinas só funcionam 10 horas por dia, qual é a produção diária atual?
Vamos resolver esse exercício de regra de três composto seguindo o passo a passo.
- Identificar as grandezas: máquinas, eficiência, produção e horas/dia.
- Identificar se as grandezas são diretamente ou inversamente proporcionais em relação à grandeza com a incógnita.
- Identificar os valores vinculados às grandezas e montar a regra de três.
6 – Em uma viagem, o motorista manteve a velocidade constante em 80 km/h. Nessa velocidade o motorista gastou 65 minutos. Qual é a velocidade necessária para fazer o percurso em 50 minutos?
- Identificar as grandezas: velocidade e tempo.
- Identificar se as grandezas são diretamente ou inversamente proporcionais em relação à grandeza com a incógnita.
- Identificar os valores vinculados às grandezas e montar a regra de três.
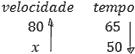
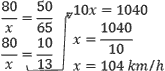
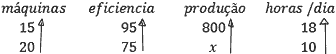
Nossa a melhor explicação de matemática que eu já vi excelente 😁
N o exercício 3 durante a simplificação de 7/5 * 50/70 obtive 1 logo x=5.
N o exercício 3 durante a simplificação de 7/5 * 50/70 obtive 1 logo x=5.
No exercício 3 durante a simplificação de frações obtive que 7/5 * 70/50 = 1, logo x=5.
otima explicação da materia e dos exercicios!
Obrigado!!
muito bom mesmo