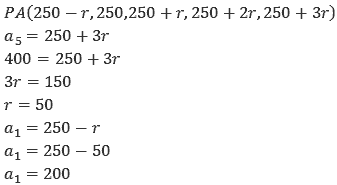PA Exercícios Resolvidos

PA Progressão Aritmética é uma sequencia numérica em que os termos, a partir do segundo, é dado pela soma do termo anterior com uma constante denominada razão da PA. Se você ainda não estudou a teoria veja no artigo PA – Progressão Aritmética.

Artigos relacionados:

• PA – Progressão Aritmética
• PG progressão geométrica
• PG exercícios resolvidos

Exercício 01 – (UFRGS) Em uma Progressão Aritmética, em que o primeiro termo é 23 e a razão é -6, a posição ocupada pelo elemento -13 é:

a) 8ª
b) 7ª
c) 6ª
d) 5ª
e) 4ª

Esse exercício é pura aplicação da fórmula do termo geral da PA. O enunciado nos forneceu todos os elementos da fórmula, exceto o número de termos. Vamos substituir na fórmula os dados do exercício e isolar n.

Exercício 2 – (UCS) O valor de x para que a sequência (2x, x+1, 3x) seja uma PA é:

a) 1/2
b) 2/3
c) 3
d) 1/2
e) 2

Sabemos que a razão da PA é uma constante, portanto vamos igualar a razão calculando ela de duas formas: 2º termo menos o 1º termo e o 3º termo menos o 2º termo. Feito isso, basta isolar x.

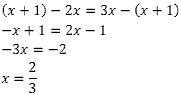
Exercício 3 – (FUVEST) Em uma progressão aritmética de termos positivos, os três primeiros termos são 1 – a, -a, . O 4° termo é:

a) 2
b) 3
c) 4
d) 5
e) 6

Vamos iniciar o exercício calculando a razão. Vamos pegar o 2º termo e subtrair o 1º termo.

Feito isso, vamos calcular o 3º termo somando o segundo termo mais a razão. Encontrando o 3º termo, vamos iguala-lo ao 3º termo informado pelo exercício e vamos elevar os dois ao quadrado para sumirmos com a raiz quadrada.

Você pode resolver a equação do 2º grau de diversas formas, mas aqui eu escolhi resolver por soma e produto.

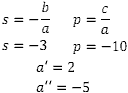
Para saber qual é a resposta certa, devemos verificar qual delas atende às duas restrições geradas por conta da raiz quadrada. Por se tratar de termos positivos, o número dentro da raiz quadrada não pode ser negativo senão torna-se número complexo. Qualquer que seja o número dentro da raiz quadrada, o resultado deve ser maior ou igual a zero. Com isso, temos essas duas restrições:

Vamos testar a=2.
11-2=9 e -2-1=-3. Observem que o segundo resultado foi menor do que zero, portanto não satisfaz a restrição. Descartamos 2 como resposta.
Vamos testar a=-5.
11-5=6 e –(-5)-1=4. As duas restrições foram satisfeitas, portanto a=-5.
Agora temos a razão e o valor de a. Nem é preciso aplicar fórmula:

Portanto: PA(6,5,4,3…)
Letra b.
Se você não conseguiu resolver esse exercício, não desanime, pois ele é considerado difícil.

Exercício 4 – (PUC-RIO 2009) Temos uma progressão aritmética de 20 termos onde o 1º termo é igual a 5. A soma de todos os termos dessa progressão aritmética é 480. O décimo termo é igual a:

a) 20
b) 21
c) 22
d) 23
e) 24

Os dados fornecidos pelo exercício são:

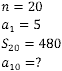
Vamos iniciar calculando o vigésimo termo da PA.

Vamos calcular a razão da PA.

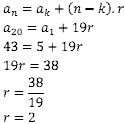
Agora vamos calcular o décimo termo da PA.

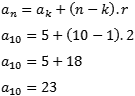
Exercício 5 – (UDESC 2008) A soma dos quatro primeiros termos de uma progressão geométrica (PG) de razão 3 é igual a 60, e a soma dos quatro primeiros termos de uma progressão aritmética (PA) também vale 60. Sabe-se que o primeiro termo da PA é igual ao primeiro termo da PG. A razão da PA é:

a) -3
b) 3/2
c) 3
d) 2/3
e) 9

Esse exercício envolve um pouco de PA – Progressão Geométrica – mas é muito bom. Vamos escrever a PG em função do seu primeiro termo, depois somamos os quatro primeiros termos e igualamos a 60. Resolvendo esse problema, calculamos o 1º termo da PG. O 1° termo da PG é igual ao 1º termo da PA, logo já sabemos o valor do 1º termo da PA. Vamos somar os 4 primeiros termos da PA e igualar a 60. Resolvendo esse problema encontramos a razão da PA. Vejam:

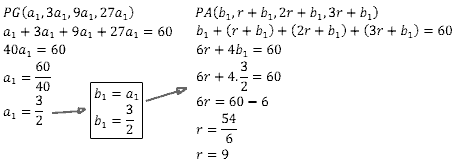
Exercício 6 – (Fuvest 2012) Considere uma progressão aritmética cujos três primeiros termos são dados por a₁ = 1 + x, a₂ = 6x, a₃ = 2x² + 4 em que x é um número real. Determine os possíveis valores de x.

Vamos usar o mesmo princípio utilizado no exercício 2. a₂-a₁=a₃-a₂. A maior dificuldade nesse exercício vai ser resolver a equação do 2º grau.

Exercício 7 – (ITA/2000) O valor de n que torna a sequência (2 + 3n; –5n; 1 – 4n) uma progressão aritmética pertence ao intervalo:

a) [– 2, –1]
b) [– 1, 0]
c) [0, 1]
d) [1, 2]
e) [2, 3]
O raciocínio para resolver esse exercício é o mesmo dos exercícios 2 e 6.

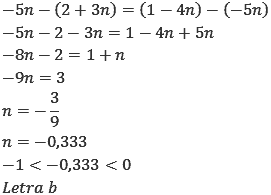
Exercício 8 – (UFG-GO) Sabendo-se que o quinto e o oitavo termo de uma PA crescente são as raízes da equação x²-14x+40=0, qual o terceiro termo dessa PA?

Para resolver esse exercício é indispensável saber calcular equação do 2º grau. O primeiro passo é resolver a equação do 2º grau. Vou resolver utilizando soma e produto.

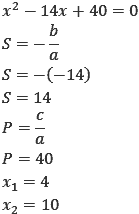
Concluímos que, por se tratar de uma PA crescente, o 5º termo da PA é 4 e o 8º termo é 10. Agora vamos escrever a PA em função da razão e calcular a razão e o 3º termo.

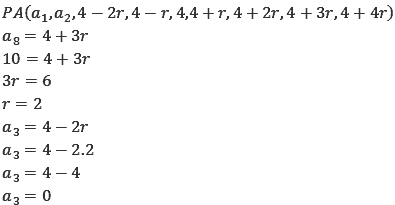
Exercício 9 – (PUC-SP) As quantias em reais de cinco pessoas estão em progressão aritmética. Se a segunda e a quinta possuem, respectivamente, R$250,00 e R$400,00, quanto a primeira possui?

Vamos escrever a PA em função da razão e dos valores conhecidos. Observem que é parecido com o exercício anterior.