PG – Progressão Geométrica

Progressão geométrica é uma sequência numérica em que os termos, a partir do segundo, são obtidos pelo produto de razão geométrica (q) com o termo anterior.

Dessa forma, a PG pode ser crescente, decrescente, oscilante ou constante, dependendo se a razão geométrica.

Em uma PG crescente, os números sequenciais são sempre maiores do que o número anterior, sendo a razão geométrica e o primeiro termo sempre maiores do que zero (q>0 e a₁>0). Ex.: PG(2,6,18,54,162,…)(q=3).

Por outro lado, a PG decrescente tem os números sequenciais menores do que o número anterior, sendo a razão geométrica sempre maior do que zero (q>0). Ex.: PG(-2,-6,-18,-54,-162,…)(q=3) ou PG(100, 50, 25,…)(q=0,5).

Já na PG oscilante, a sequência é composta por números intercalados entre positivos e negativos, sendo a razão geométrica sempre menor do que zero (q<0). Ex.: PG(-2,+6,-18,+54,-162,…)(q=-3).

Por último, na PG constante todos os termos da sequências são iguais, sendo a razão geométrica sempre igual a um (q=1). Ex.: PG(3,3,3,3,3,…)(q=1)

Artigos relacionados:

• PG exercícios resolvidos
• PA Progressão Aritmética
• PA exercícios resolvidos

Fórmula da Razão da PG

A chamada razão da PG é uma constante representada geralmente pela letra ‘q’. É a partir da razão da PG que será determinado todos os termos, portanto ela é parte fundamental da PG.
A razão da pg (q), também conhecida como razão geométrica, é calculada fazendo a divisão de qualquer termo, exceto o 1º termo, pelo termo anterior. A fórmula da razão da PG é:

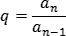
Exemplo de como calcular a razão da PG

Encontre a razão geométrica da seguinte PG( 2, 6, 18, 54 ).
Utilizando a fórmula da razão da PG, vou calcular de 3 formas. Observem que o resultado é sempre o mesmo.

Assim mostramos que a razão dessa PG é 3 e que não importa qual termo escolhemos, desde que não seja o 1º. Se for feita a divisão com o termo anterior a ele, o resultado será sempre o mesmo. Portanto a razão da PG é uma constante.

Fórmula Progressão Geométrica

A progressão geométrica possui diversas fórmulas, sendo que as principais estão representadas abaixo:

Em que,

­a_n: N ésimo termo da PG (termo qualquer da PG – o termo que quer encontrar);
a_k: K ésimo termo da PG (termo qualquer da PG – você deve conhecer o valor desse termo);
q^(n-k): razão da PG elevada a diferença de n-k.

Soma dos Termos da PG

Soma de todos os termos da PG

A fórmula a seguir nos retorna como resposta a soma de todos os termos da PG.

Soma dos termos em um intervalo da PG

A fórmula seguinte nos retorna como resposta a soma dos termos em um intervalo de ‘r’ a ‘t’.

Soma dos termos de uma PG decrescente e infinita

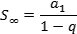
Para uma PG ser decrescente a razão geométrica tem que estar no intervalo: 0 < q < 1, ou seja, maior do que 0 e menor do que 1. Sabendo que a PG é infinita e decrescente, então o último termo a_n será zero. A fórmula da soma dos termos de um PG infinita e decrescente é: