Como simplificar frações

Como simplificar frações é uma das etapas mais importantes da matemática, porque torna os cálculos mais rápidos e fáceis de entender. Quando você simplifica uma fração, está reduzindo seus números para a menor forma possível, sem alterar o valor real dela.

Isso faz toda diferença em contas longas, como multiplicações ou expressões numéricas. Se você ainda está aprendendo os fundamentos, vale a pena conferir o guia como aprender fração, onde explicamos o que é fração, como calcular e quando usar o MMC — conceito essencial para entender o processo de simplificação.

Por que simplificar frações é tão importante?

A grande vantagem da simplificação é reduzir os números a serem trabalhados.
Na prática, números menores são muito mais simples de manipular e deixam as operações mais leves.

Imagine resolver a conta:
729/18 × 48/18

Fazer 729 × 48 e depois dividir o resultado por 18 não é nada agradável. Mas, se simplificarmos antes, a conta fica muito mais fácil. Essa é a ideia: eliminar o excesso para facilitar a vida. E para visualizar isso de forma prática, use nossa calculadora de multiplicação de fração, uma calculadora que mostra o passo a passo da operação e ajuda a compreender como a simplificação transforma cálculos grandes em resultados simples. Ao testar, você vai perceber que a calculadora é uma aliada poderosa para aprender e praticar simplificações de maneira rápida e intuitiva.

Como simplificar uma fração na prática

Simplificar é fácil: basta dividir o numerador e o denominador pelo mesmo número, até que não seja mais possível simplificar. Esse número é chamado de divisor comum.

1. Comece pelos divisores mais simples

Tente dividir por 2, 3, 5 ou 7, pois são os divisores mais comuns. Continue testando até que a fração fique “irredutível”.

Exemplo:
Simplifique 24/36
Dividindo ambos por 2 → 12/18
Depois por 2 novamente → 6/9
E por fim por 3 → 2/3

Ou seja, 24/36 é equivalente a 2/3, que é a forma mais simples da fração. Esse tipo de raciocínio é a base para entender qualquer operação com frações, como mostramos também em Fração Exercícios Resolvidos.

Simplificando frações com mais de uma operação

Quando há mais de uma fração em uma mesma conta, é possível simplificar qualquer número de cima com qualquer número de baixo, desde que eles tenham um divisor comum. Isso vale, por exemplo, em expressões como multiplicações ou divisões.

Exemplo:
Simplifique 7/8 × 8/9 × 9/7

Observe o que acontece:
O 7 de cima cancela com o 7 de baixo, o 8 de cima com o 8 de baixo, e o 9 de cima com o 9 de baixo. No final, sobra apenas 1/1, ou seja, o resultado é 1. Esse tipo de simplificação é muito útil antes de realizar uma multiplicação, pois evita lidar com números grandes. Você pode ver mais exemplos aplicados no artigo como tesolver expressões numéricas com fração, que mostra como simplificar dentro de parênteses e colchetes.

Simplificar antes de calcular é um ótimo atalho

Uma boa prática é simplificar a fração antes de começar o cálculo. Isso vale para somas, subtrações, multiplicações e divisões. Além de reduzir o tamanho dos números, a simplificação ajuda a visualizar o raciocínio. Por exemplo, quando os denominadores são diferentes, é possível combinar o uso do MMC com a simplificação para chegar ao resultado correto com menos esforço.
Se tiver dúvidas sobre como achar o mínimo múltiplo comum, dê uma olhada no MMC de Fração.

Exemplos resolvidos de simplificação

Exemplo 1:

Simplifique 10/15
→ Divida o numerador e o denominador por 5
10 ÷ 5 = 2
15 ÷ 5 = 3
✅ Resultado: 2/3

Exemplo 2:

Simplifique 14/28
→ Divida por 2: 7/14
→ Divida por 7: 1/2

Exemplo 3:

Simplifique 45/60
→ Divida por 5: 9/12
→ Divida por 3: 3/4

Se quiser mais exercícios como esses, acesse a página Fração Exercícios Resolvidos, que traz vários exemplos com explicações detalhadas.

Erros mais comuns sobre como simplificar frações

Mesmo sendo simples, a simplificação de frações pode gerar erros se feita com pressa. Veja os mais comuns:

Dividir apenas um dos números.
Lembre-se: é sempre o numerador e o denominador juntos.
Parar de simplificar antes da hora.
Às vezes dá para reduzir ainda mais, então revise seu resultado.
Esquecer de observar o sinal.
Se um dos termos for negativo, o sinal deve ser mantido corretamente no final.

Evitar esses erros é fundamental para resolver expressões maiores — e você pode praticar com exemplos no artigo Como Resolver Expressões Numéricas com Fração, que mostra situações completas de simplificação dentro de contas.

Regras da simplificação de fração

a) Em uma fração simples, divida o número de cima pelo número de baixo. Quando forem números maiores, tente começar dividindo por números menores como 2, 3, 5 e 7, até diminuir para números irredutíveis.

No exemplo acima, fui dividindo por 2 até chegar na forma irredutível da fração.
b) Quando tem mais de uma fração, podemos simplificar qualquer número de cima com qualquer número de baixo.

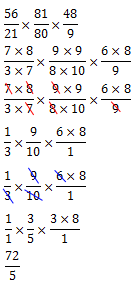
Observem que decompus os números maiores em números menores para facilitar a visualização das simplificações. Na primeira fração, simplifiquei o 7 em cima com o 7 em baixo; simplifiquei o 8 de cima da primeira fração como o 8 de baixo da segunda fração; cortei (simplifiquei) o 9 de cima da segunda fração com o 9 de baixo da terceira fração. Portanto, podemos simplificar quaisquer números de cima com qualquer número de baixo (desde que tenham um divisor comum), não importando a qual fração pertença.

Simplificar é tornar a matemática mais leve

Simplificar frações é um hábito que deixa qualquer cálculo mais simples e rápido.
Além de economizar tempo, essa técnica melhora o entendimento dos números e ajuda a evitar erros em operações mais longas.
Com o tempo, você vai perceber que simplificar é o primeiro passo para dominar de verdade o raciocínio matemático.

Continue aprendendo sobre frações

Para avançar nos seus estudos, explore os outros conteúdos do Como Calcular e pratique com nossas ferramentas:

Simplificar é entender. E quanto mais você pratica, mais fácil a matemática se torna.