FÓRMULA DA FORÇA ELÁSTICA
Ao todo, são duas fórmulas que devemos saber sobre força elástica. Entretanto, pode ser necessário o conhecimento de outras fórmulas para resolver os exercícios.

01 – (UFG) Para proteção e conforto, os tênis modernos são equipados com amortecedores constituídos de molas. Um determinado modelo, que possui três molas idênticas, sofre uma deformação de 4 mm ao ser calçado por uma pessoa de 84 kg. Considerando-se que essa pessoa permaneça parada, a constante elástica de uma das molas será, em kN/m, de
a) 35,0
b) 70,0
c) 105,0
d) 157,5
e) 210,0
Quando a pessoa calça o tênis transforma energia gravitacional em energia elástica. No exercício é citado que o tênis possui 6 molas no total, 3 em cada pé. A força peso total exercida sobre as molas é:
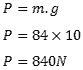
A força peso total é de 840N. Dividindo a força peso total pela quantidade de molas temos a força peso aplicada sobre cada mola, o que faz ela sofrer a deformação. Portanto, a força peso aplicada sobre a mola é igual força elástica necessária para deformar a mola. Assim, vamos igualar a fórmula da força elástica com a força peso.

02 – (UPE) Um corpo de massa m está suspenso por duas molas ideais, paralelas, com constantes elásticas k e deformadas de d. Sabendo que o sistema se encontra em equilíbrio, assinale a alternativa que expressa k. Dado: Considere a aceleração da gravidade g.
a) 2mg/d
b) mg/d
c) mg/2d
d) 2d/mg
e) mg
Analisando o exercício temos a força peso P puxando as molas para baixo e duas molas exercendo força elástica para cima. Como é mantido o equilíbrio, então a força peso é igual à soma da força elástico das molas.

03 – Uma mola tem constante elástica K=4,0kN/m. Quando ela for comprimida em 50cm, qual será a força elástica?
Esse exercício é bem simples, mas é preciso prestar atenção para a unidade de medida. A constante elástica esta em ‘m’ e a compressão da mola está em ‘cm’. Nesse caso vamos passar ‘cm’ para ‘m’ e depois basta aplicar a fórmula da força elástica:
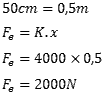
04 – Calcule a força elástica necessária para comprimir 30cm de uma mola cuja constante elástica é K=1,2kN/m.
Novamente um exercício de fixação da fórmula da força elástica. Assim como no exercício anterior vamos igualar as unidade de medida, passando os 30cm para metros. Feito isso aplicamos a fórmula da força elástica:
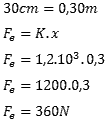
5 – Uma pessoa com massa de 80Kg está sobre uma plataforma cuja base é formada por 4 molas idênticas. Calcule a constante elástica das molas, sabendo que as molas sofreram deformação de 2cm.
O primeiro passo para resolver esse exercício é calcular a força peso sobre a plataforma. Feito isso, vamos dividir essa força por quatro, que é a quantidade de molas, ou seja, são quatro molas que exercem força elástica em direção oposta a força peso. A soma das quatro forças elásticas é igual a força peso.

Agora vamos calcular a força elástica de cada mola:
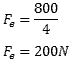
Por último, aplicamos a fórmula da força elástico isolando a constante elástica. Lembre-se de passar a deformação da mola de centímetros para metros. Para isso, basta dividir por 100.
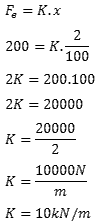
5 está errada, pois a constante x é transfomada pra m e n decametro, ou seja, divide por 10 e n por 100.. resposta 1000 n ou 1kn/m
primeira questão ta errada a resolução, vc tem que passa 4mm para metros.
Larissa, ele transformou e escreveu como uma potência de 10.
4 mm = 0,004 m = 4×10-³m
PESSOAL PRECIZO DE AJUDA AQUI!!!!!
No sistema ao lado, as molas ideais têm,
cada uma, constante elástica igual a 2000 N/m e comprimento natural 10 cm. Se cada um dos corpos A e B
tem massa igual a 5 kg, então a soma LA + LB vale:
a) 30,0 cm
b) 27,5 cm
c) 25,0 cm
d) 22,5 cm
e) 20,0 cm
Dado: g = 10 m/s2.
Mas e se eu quiser achar o x (deformação da mola) em mm com o k (constante elástica da mola) em N/m ?
♥♥otimo mas pode ficar melhor so precisa q as espicaçoes sejam mas esplicita
Seu português também
oi
idiota hein você, a menina elogia a merda desse site, e ainda leva carão por não ter um português muito bom, mas idai? pelo menos ela tem caráter…Deixa ela ser feliz, desocupado(a) viu você.
Muito Bom!
Conteudo muito claro e explicativo. Parabéns!
a 4 nao era para dar 4000n ???
pois 12/3 =4
1200/0,3=4000
e so multiplicar por 1000 e temos 4kn
mtooo bom!!!!
Ameiii <3
mt obrigada
Parabéns pelo conteúdo e muito obrigado. Perfeito para aprender o passo a passo.
Ótimo os exercícios, as resoluções ajudam bastante quando se tem dúvida. Obrigada
Muito bom cara vlw ajudou mt; excelente trabalho continue assim! 😉
Não entendi o porquê do 1,2 ser multiplicado por 10³ e nem por que 4,0 ter acontecido a mesma coisa.
tbm nao entendi
É por causa daquele “K” que vem depois do número. Ele sinaliza que deve ser multiplicado por 10³, pois o N é a unidade central, como o metro… repare no sistema métrico decimal:
km hm dam m dm cm mm
Agora vamos substituir o Metro por Newton:
kN hN daN N dN cN mN
Do “kN” até o Newton são três casas, certo? Então, se multiplicarmos “kN” por 1000 (10³), chegaremos ao “N”.
Resumindo: são dois jeitos de escrever valores para força, mas que, no final, tem as mesma intensidades.
Resumindo é mil
Tipo 4,0 fica 4000 e 1,2 fica 1200
simpris
Muito útil! Obrigado!