Como calcular a matriz inversa

Vou ensinar nesse post como calcular a matriz inversa de uma determinada matriz. Para que uma matriz seja inversa a outra matriz é preciso que o produto das duas matrizes seja igual à matriz identidade e que as matrizes sejam matrizes quadradas. Vamos aos exemplos:

Exemplo 1: Temos a matriz A e  a matriz B. Vamos verificar se elas são matrizes inversas uma da outra.

A = B=

Primeiro passo:

Vamos multiplicar A x B:

x = =

Segundo passo:

Verificamos se o resultado do produto A x B é igual a matriz identidade. Se for igual a matriz identidade, então elas são matrizes inversas uma da outra, mas se não for, então elas não são matrizes inversas uma da outra. No nosso exemplo a matriz do produto A x B é diferente da matriz identidade. Isso significa que A e B não são matrizes inversas uma da outra.

Exemplo 2: Temos a matriz C e queremos encontrar a inversa dela.

C= D=

Primeiro passo:

Vamos multiplicar C x D:

x =

Segundo passo:

Igualar o resultado do produto C x D com a matriz identidade:

=

Assim podemos montar um sistema com quatro variáveis e quatro equações.

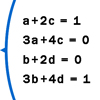
Agora é só resolver o sistema, obter o valor de ‘a’, ‘b’, ‘c’, ‘d’ e substituir na matriz.

a + 2c = 1
a = 1 – 2c
3a + 4c = 0
3(1 – 2c) + 4c = 0
3 – 6c + 4c = 0
3 – 2c = 0
-2c = -3
c = 3/2
a = 1 – 2c
a = 1 – 2(3/2)
a = 1 – 6/2
a = 1 – 3
a = -2

b + 2d = 0
b = -2d
3b + 4d = 1
3(-2d) + 4d = 1
-6d + 4d = 1
-2d = 1
d = -1/2
b = -2d
b = -2(-1/2)
b = 2/2
b = 1