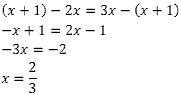Mestre Calculadora

PA Progressão Aritmética é uma sequencia numérica em que os termos, a partir do segundo, é dado pela soma do termo anterior com uma constante denominada razão da PA. Se você ainda não estudou a teoria veja no artigo PA – Progressão Aritmética.

Artigos relacionados:

• PA – Progressão Aritmética
• PG progressão geométrica
• PG exercícios resolvidos

Exercício 01 – (UFRGS) Em uma Progressão Aritmética, em que o primeiro termo é 23 e a razão é -6, a posição ocupada pelo elemento -13 é:

a) 8ª
b) 7ª
c) 6ª
d) 5ª
e) 4ª

Esse exercício é pura aplicação da fórmula do termo geral da PA. O enunciado nos forneceu todos os elementos da fórmula, exceto o número de termos. Vamos substituir na fórmula os dados do exercício e isolar n.

Exercício 2 – (UCS) O valor de x para que a sequência (2x, x+1, 3x) seja uma PA é:

a) 1/2
b) 2/3
c) 3
d) 1/2
e) 2

Sabemos que a razão da PA é uma constante, portanto vamos igualar a razão calculando ela de duas formas: 2º termo menos o 1º termo e o 3º termo menos o 2º termo. Feito isso, basta isolar x.

Ler mais

A pirâmide é uma figura geométrica muito importante. Nessa página, vou disponibilizar exercícios resolvidos passo a passo sobre pirâmides para auxiliar no aprendizado da matéria. Aqui você vai encontrar exercícios de autoria própria e exercícios de vestibulares e concursos. Além disso, muitos exercícios sobre as pirâmides exigem conhecimento de outras matérias como o Teorema de Pitágoras.

Exercício 01 – Considere uma pirâmide triangular. Sabe-se que a altura da pirâmide é de 5m e a aresta lateral mede 9m. Calcule a medida do centro da base até um vértice da base.

Como vimos no post sobre pirâmides, a altura, aresta lateral e a medida do centro da base até um vértice qualquer da base formam um triângulo retângulo. Dessa forma, tendo dois lados desse triângulo retângulo podemos aplicar o Teorema de Pitágoras para calcular o terceiro lado.

Exercício 02 – Uma pirâmide de base quadrada tem 18m de altura e 20m de apótema lateral. Calcule a área da base e o volume da pirâmide.

Com essas informações vamos utilizar o Teorema de Pitágoras e calcular o apótema da base. Sabendo que o apótema da base é a metade do lado da base , então calculamos a medida do lado da base (aresta da base). Por último, calculamos a área da base. A área do quadrado é igual ao quadrado do lado da base.

O volume da pirâmide ficou fácil de calcular porque já temos todos os dados necessários: área da base e altura.

Ler mais

Exercício 01 – Ache a equação reduzida da reta que passa pelos pontos P(0,1) e Q(1,2).

Exercício 02 – Calcule a equação reduzida da reta que intercepta os pontos P(-1,4) e Q(2,-2).

Ler mais

Exercício 01- I

Exercício 01- II

Exercício 02

Ler mais