Regra de três composta é um método matemático utilizado para calcular o valor de uma grandeza a partir da relação existente com outras grandezas. Além disso, a regra de três composta pode ser diretamente ou inversamente proporcional.
- Regra de Três Exercícios Resolvidos
- Regra de Três Simples
- Regra de Três Composta Exercícios Resolvidos
Como resolver regra de 3 composta

Como fazer regra de três composta?
Identificar as grandezas
Grandeza é tudo aquilo que pode ser medido ou quantificado, tais como velocidade, eficiência, quantidade de pessoas, peso, etc.
Considere o seguinte exercício como exemplo: Se 12 técnicos analisam 400 processos em 5 dias, trabalhando 6 horas por dia, então quantas horas por dia devem trabalhar 10 técnicos, por 3 dias, para analisar 100 processos?
As grandezas são: “técnicos”, “processos”, “dias” e “horas por dia”
Identificar a grandeza da incógnita
No caso é a grandeza “horas por dia”, visto que para todas as grandezas são informados dois valores, exceto para horas por dia. Nesse caso, devemos calcular a quantidade de horas por dia de trabalho necessária para que 10 técnicos analisem 100 processos em 3 dias.
Determinar se as demais grandezas são diretamente ou inversamente proporcional à grandeza da incógnita
Para isso, é melhor elaborar uma frase do tipo:
* Se aumentar a quantidade de horas por dia de trabalho, precisará (aumentar ou diminuir) a quantidade de técnicos? Assim, se aumentar a jornada diária de trabalho, menos técnicos serão necessários para executar o mesmo serviço. Portanto, são inversamente proporcionais.
* Se aumentar a quantidade de horas por dia de trabalho, analisarão (maior ou menor) quantidade de processos? Certamente analisarão maior quantidade de processos. Portanto, são diretamente proporcionais.
* Se aumentar a quantidade de horas por dia de trabalho, (mais ou menos) dias de trabalho serão necessários? Se trabalhar mais por dia, acaba mais rápido. Portanto, são inversamente proporcionais.
Montar a tabela da regra de três composta, pois facilita ao visualizar os dados organizados.
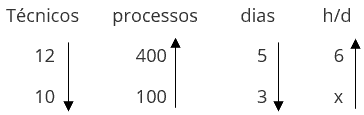
Como montar a tabela da regra de três composta:
1 – Escreva o nome das grandezas, não importa a ordem.
2 – Na primeira linha, coloque os valores abaixo das respectivas grandezas.
3 – Na segunda linha, coloque os valores abaixo das respectivas grandezas, deixando uma incógnita no lugar do valor que será calculado.
4 – Coloque uma seta para cima ao lado da grandeza que possui a incógnita.
5 – Coloque setas nas demais grandezas, sendo que a seta será para cima caso seja diretamente proporcional ou para baixo se for inversamente proporcional.
Montar a relação matemática
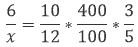
Como montar a equação da regra de três composta:
1 – Coloque os valores da grandeza com incógnita do lado esquerdo da igualdade.
2 – Do lado direito, multiplique os demais valores, sendo que os valores referentes a grandezas diretamente proporcionais devem ser informados da forma que estão, enquanto que os valores das grandezas inversamente proporcionais devem ser invertidos (numerado com denominador).
Resolver a equação
Neste caso, a resposta é 3.
Concluímos que 10 técnicos analisam 100 processos em 3 dias trabalhando 3 horas por dia.
Exemplo de regra de três composta
Para concluir uma obra em 12 dias é necessário 4 operários trabalhando 6 horas por dia. Em quantos dias será possível concluir a obra se trabalharem 10 operários, 8 horas por dia?
Grandezas: Dias, Operários e Horas por Dia (h/d)

Agora colocamos as setas, indicando se são diretamente ou inversamente proporcionais. Essa relação tem sempre que ser entre a grandeza com a incógnita e a sem incógnita. No nosso caso a comparação é entre (Dias x Operários) e (Dias x h/d).
Quanto mais operários mais dias para terminar a obra?
Quanto mais h/d mais dias para terminar a obra?
Em ambos os casos a resposta é não, logo as grandezas Operários e h/d são inversamente proporcionais à grandeza Dias.


Show