A equação reduzida da reta é uma função em que o eixo y (ordenadas) é dado em função do eixo x (abscissas). Dessa forma, dado um valor do eixo x podemos achar o valor do eixo y e marcar o ponto (x,y). Por se tratar de uma reta, a equação reduzida da reta sempre será uma equação do primeiro grau. Portanto a equação reduzida da reta terá o seguinte formato:
Em que,
y: valor do eixo y;
m: coeficiente angular;
x: valor do eixo x;
c: constante.
Observem que “c” é uma constante e determina o valor de y, quando o valor de x é igual a zero.
Coeficiente angular
O coeficiente angular indica a inclinação da reta. O cálculo do coeficiente angular pode ser feito de duas formas: através do ângulo de inclinação ou por meio de dois pontos da reta. A decisão de qual método utilizar, vai depender dos dados que você possuir sobre o exercícios. As duas fórmulas do coeficiente angular são:
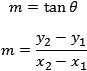
Observando a inclinação da reta, podemos tirar as seguintes conclusões sobre o sobre coeficiente angular:
- Se
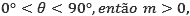coeficiente angular positivo; - Se
coeficiente angular negativo; - Se
coeficiente angular igual a zero; - Se
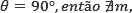não existe coeficiente angular.
Como achar a equação reduzida da reta
Para achar a equação reduzida da reta, é preciso que já tenha calculado o coeficiente angular. A fórmula da equação reduzida da reta é:
Em que,
y: valores do eixo y;
x1 e y1: coordenadas de um ponto qualquer da reta;
m: coeficiente angular.
Equação reduzida da reta exercícios resolvidos passo a passo
Exemplo: Encontre a equação reduzida da reta que passe pelos pontos P(2,3) e Q(3,5).
1º Passo: Calcular o coeficiente angular (m).
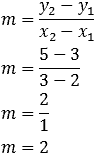
2º Passo: Calcular a equação da reta.
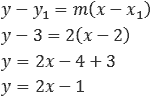
Veja também:
To interesado em aprender o passo a passo do site