Multiplicar frações é muito mais simples do que parece — e com uma calculadora de multiplicação de fração, fica ainda mais rápido.
Essa operação é uma das mais diretas da matemática, e entender como ela funciona é essencial para resolver qualquer tipo de exercício de fração com confiança.
Você vai aprender como multiplicar frações manualmente, simplificar o resultado, transformar em decimal ou porcentagem e usar nossa calculadora para confirmar cada passo.
Se você ainda está aprendendo o básico sobre o que é uma fração, recomendo começar pelo artigo como aprender fração, onde explicamos de forma simples como numerador e denominador funcionam.
O que é uma fração e por que ela é importante na multiplicação?
Uma fração representa uma parte de um todo. O número de cima (numerador) mostra quantas partes você tem, e o número de baixo (denominador) indica em quantas partes o todo foi dividido.
Por exemplo, ¾ significa “3 partes de um total de 4”.
As frações ajudam a trabalhar com partes menores que 1, e tornam cálculos mais precisos — especialmente em medições, proporções e porcentagens. Elas também facilitam o raciocínio em operações mais complexas, como multiplicações sucessivas ou expressões com frações.
Você usa multiplicações de frações mais do que imagina: ao dobrar receitas, calcular descontos, proporções em construções, ou ajustar medidas. Saber multiplicar frações é essencial para fazer essas contas corretamente.
Como fazer multiplicação de fração passo a passo?
Multiplique numerador com numerador e denominador com denominador.
Exemplo:
23×45=815\frac{2}{3} × \frac{4}{5} = \frac{8}{15}32×54=158
Não há necessidade de calcular o MMC — ele só é usado em soma e subtração de frações.
Diferente da soma, a multiplicação não exige denominadores iguais. Você trabalha com os valores de forma direta, o que torna essa operação uma das mais simples de todas.

E pronto — a multiplicação está resolvida. Depois disso, basta verificar se o resultado pode ser simplificado, como ensinamos em Como Simplificar Frações.
Se quiser praticar, veja mais exemplos em exercícios de fração.
A calculadora de multiplicação de fração é uma ferramenta que faz tudo automaticamente — ideal para conferir o resultado ou estudar o processo passo a passo.
Digite o numerador e o denominador das duas frações, e clique em “Calcular”.
A ferramenta faz a multiplicação e já entrega o resultado simplificado.
Além da fração final, a calculadora exibe o número decimal equivalente e, em alguns casos, até a porcentagem.
Isso ajuda a visualizar melhor o valor obtido.
Como multiplicar fração por número inteiro?
Todo número inteiro pode ser escrito como uma fração com denominador 1.
Por exemplo, 6 é o mesmo que 6/1.

Após multiplicar, verifique se a fração pode ser simplificada.Na calculadora, o resultado já aparece reduzido automaticamente.
Como simplificar frações antes da multiplicação?
Simplificar antes evita lidar com números grandes e torna as operações mais rápidas e fáceis.

No primeiro passo, dividimos o numerador e denominador de vermelho por 2 e o de azul por 3. Em seguida, repetimos o processo e dividimos os números em vermelho por 2 novamente. Por fim, obtivemos o resultado simplificado.
Divida o numerador pelo denominador:
2/5 = 0,4
7/8 = 0,875
Multiplique o resultado decimal por 100 e adicione o símbolo “%”.
2/5 = 0,4 = 40%
|
Fração |
Decimal |
Porcentagem |
|
1/2 |
0,5 |
50% |
|
3/4 |
0,75 |
75% |
|
2/5 |
0,4 |
40% |
|
7/8 |
0,875 |
87,5% |
Mesmo que os denominadores sejam diferentes, o processo é o mesmo — basta multiplicar direto. O MMC não é usado aqui, mas é essencial em outras operações, como mostra o artigo MMC de fração.
Após o cálculo, veja se é possível dividir numerador e denominador pelo mesmo número. Assim, a fração fica reduzida à forma mais simples.
Quais erros evitar ao multiplicar frações?
O vídeo abaixo, ensina através de exemplos. Configurei para iniciar na parte da multiplicação, mas fique à vontade para assistir inteiro.
Para resolver esse exercício, vamos multiplicar as frações, sendo que numerador com numerador e denominador com denominador.
Numeradores: 5 . 9 = 45
Denominadores: 8 . 7 = 56
Portanto, a resposta é 45/56.
Ao perceber que todos os números são pares, é certeza que é possível simplificar a fração. Nesse caso, poderia simplificar por 2 diversas vezes, mas vamos simplificar o numerador 48 e o denominador 24 por 24. Além disso, simplificaremos 8 e 2 por 2.
48/8 . 2/24
2/4 . 1/2
Ainda podemos simplificar por 2 antes de multiplicar as frações.
1/2 . 1/2 = 1/4
Resolva os exercícios de multiplicação de fração abaixo.
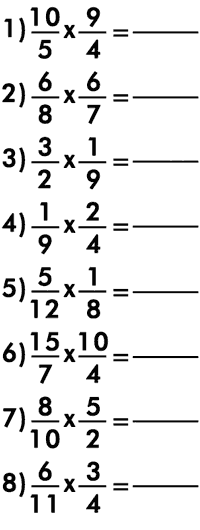
Para fixar o aprendizado, resolva exercícios e confira os resultados com nossa calculadora. Você pode começar pelos exemplos de fração exercícios resolvidos, que mostram passo a passo como chegar ao resultado certo.
E se quiser se aprofundar mais, no youtube você encontra multiplicação de frações com exemplos tem explicações detalhadas e exercícios adicionais.
Multiplicar frações é uma das etapas mais importantes para dominar as operações matemáticas. Continue aprendendo com nossos conteúdos: