 A probabilidade é uma matéria muito presente nos concursos públicos e vestibulares. Não é uma das matérias mais simples de se estudar e exige dedicação para aprender. Estude os conceitos e entenda como funciona, depois passe a resolver exercícios. A melhor maneira de aprender é resolvendo exercícios. Nessa página, vou disponibilizar exercícios resolvidos. Aos poucos vou adicionando mais exercícios.
A probabilidade é uma matéria muito presente nos concursos públicos e vestibulares. Não é uma das matérias mais simples de se estudar e exige dedicação para aprender. Estude os conceitos e entenda como funciona, depois passe a resolver exercícios. A melhor maneira de aprender é resolvendo exercícios. Nessa página, vou disponibilizar exercícios resolvidos. Aos poucos vou adicionando mais exercícios.
01 – Em um dado com seis faces numeradas de 1 a 6, a probabilidade de que cada um dos resultados ocorra é a mesma. Esse dado será lançado até que se obtenha o resultado 6. A probabilidade de que isso aconteça em, no máximo, 2 lançamentos é:
a) 1/36
b) 5/36
c) 6/36
d) 7/36
e) 11/36
![]()
O raciocínio para resolver esse exercício é pensar que para o número 6 sair em no máximo na 2º jogada só existem duas possibilidades: o 6 sair de primeira ou sair na segunda tentativa. O que temos que calcular agora é a probabilidade dessas possibilidades.
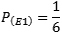
A probabilidade do 6 sair na primeira tentativa é:
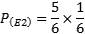
Para que o 6 saia na segunda tentativa, é preciso que na primeira tentativa saia outro número qualquer, portanto a probabilidade do 6 sair na segunda tentativa é a probabilidade de sair qualquer outro número na primeira e sair o 6 na segunda.
Agora temos que somar as duas probabilidades: ocorrer no evento 1 (E1) OU no evento 2 (E2).
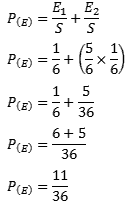
02 – São colocadas em um saco bolinhas de tênis de mesa: 5 de cor branca e 10 de cor laranja. Retira-se uma bolinha,sem reposição,e,em seguida, retira-se outra. Qual a probabilidade de serem da mesma cor?
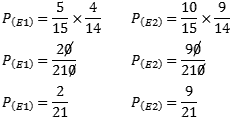
Existem duas possibilidades que atendem a exigência:
E1: 1º e 2º bolas serem brancas
E2: 1º e 2º bolas serem laranja
Agora calcularemos a probabilidade de ocorrer cada um dos eventos acima e depois somamos as probabilidades. No 1º evento temos 5 bolinhas brancas em um total de 15 bolinhas. Após retirar a 1º bolinha temos 4 bolinhas brancas e 14 bolinhas. A probabilidade do 1º evento é de 2 para 21. No 2º evento, temos 10 bolinhas laranja e 15 bolinhas no total. Depois de retirar uma bolinha laranja temos 9 bolinhas laranja e 14 bolinhas ao todo. A probabilidade do 2º evento é de 9 para 21. Somando a probabilidade do 1º evento com a probabilidade do 2º evento, encontramos a resposta do exercício.
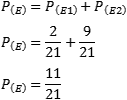
03 – Numa festa, há 10 crianças que vão ganhar 10 presentes, que estão empacotados da mesma maneira. Elas sabem que os presentes consistem em 7 caixas de bombons e em 3 jogos. Para a escolha dos presentes, os nomes das crianças serão sorteados e a criança cujo nome for sorteado escolherá um dos pacotes, sem saber o que há dentro.
O primeiro sorteado ganhou uma caixa de bombons e o segundo sorteado ganhou um jogo. Se o terceiro sorteado quer ganhar um jogo, a probabilidade de ele consegui-lo é de
- 1/4.
- 1/5.
- 1/8.
- 3/5.
- 3/10.
04 – Em um escritório, há dois porta-lápis: o porta-lápis A com 10 lápis, dentre os quais 3 estão apontados, e o porta-lápis B com 9 lápis, dentre os quais 4 estão apontados.

Um funcionário retira um lápis qualquer ao acaso do porta-lápis A e o coloca no porta-lápis B. Novamente ao acaso, ele retira um lápis qualquer do porta-lápis B.
A probabilidade de que este último lápis retirado não tenha ponta é igual a:
- 0,64
- 0,57
- 0,52
- 0,42
05 – Francisco deve elaborar uma pesquisa sobre dois artrópodes distintos. Eles serão selecionados, ao acaso, da seguinte relação: aranha, besouro, barata, lagosta, camarão, formiga, ácaro, caranguejo, abelha, carrapato, escorpião e gafanhoto.
Qual é a probabilidade de que ambos os artrópodes escolhidos para a pesquisa de Francisco não sejam insetos?
- 49/144
- 14/33
- 7/22
- 5/22
- 15/144
06 – Em uma urna, existem exatamente dezesseis bolas, entre as quais oito são vermelhas; e as outras oito, verdes. Dessa urna, será retirada ao acaso uma bola. Sua cor será registrada. Se a bola for vermelha, ela será recolocada na urna e, se for verde, será deixada fora. Uma segunda bola é, então, retirada aleatoriamente da urna, e sua cor é anotada.
Em relação a essa urna e às bolas retiradas, julgue os itens a seguir, assinalando (V) para os verdadeiros e (F) para os falsos.
A segunda bola retirada é verde, então a probabilidade de que a primeira bola retirada tenha sido vermelha é igual a 15/29.
- ( ) Certo
- ( ) Errado
07 – Para o sorteio de uma bicicleta em uma festa, haviauma urna com 100 fichas enumeradas de 1 a 100. Uma delas daria o prêmio tão esperado. A probabilidadede o número sorteado ser, ao mesmo tempo, múltiplo de 6 e 15 é:
- 0,01.
- 0,02,
- 0,03.
- 0,04.
- 0,05.
08 – O Centro Paula Souza administra Escolas Técnicas (Etecs) e Faculdades de Tecnologia (Fatecs) estaduais em 149 municípios, no Estado de São Paulo.
Para participar de um simpósio sobre educação a distância, a Fatec São Paulo enviou cinco alunos, sendo dois homens; a Fatec Sorocaba enviou três alunos, sendo uma mulher; e a Fatec da Baixada Santista enviou quatro alunos, sendo dois homens. Para a abertura desse simpósio, será selecionada, ao acaso, uma dessas Fatecs e dela se escolherá, também ao acaso, um aluno para representar o Centro Paula Souza. A probabilidade de que o aluno escolhido seja uma mulher é
- 16/45.
- 37/90.
- 19/45.
- 43/90.
- 28/45.
09 –
Em uma urna há dezoito bolas amarelas, algumas bolas vermelhas e outras bolas brancas, todas indistinguíveis pelo tato, e sabe-se que a quantidade de bolas brancas é igual ao dobro das vermelhas.
Se a probabilidade de se retirar, ao acaso, uma bola amarela da urna é 2/5, a quantidade de bolas vermelhas que há na urna é
- 8.
- 9.
- 12.
- 18.
- 24.
10 – Ao lançar um dado 3 vezes sucessivas, qual é a probabilidade de obter ao menos um número ímpar?
- 1/8
- 1/4
- 3/8
- 5/8
- 7/8
Ki bom