Noção intuitiva de limite
O limite observa o comportamento de uma função f(x), quando x tende a p.
Considere a função f(x)=x+4. Se montarmos uma tabela com valores se aproximando de f(1) pela esquerda e pela direita, vamos observar que quanto mais x tende para 1, mais f(1) tende a 5.
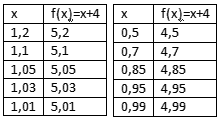
Observe que à medida que x tende a 1 (x –> 1), f(x) tende a f(1) (f(x) –> f(1)). Portanto, o limite de f(x) quando x tende a 1 é igual a 5. O limite de f(x) quando x tende a p não depende do valor que f(x) assume em p, mas sim dos valores próximos a f(p). Por isso, diz-se que limite é um conceito local.
A fórmula do limite, quando a função f é contínua no ponto p.
![]()
Propriedades dos limites
As propriedades dos limites são muito úteis na hora de resolver exercícios. Algumas propriedades são simples de aprender e memorizar. Recomendo estudar as propriedades, pois vão te ajudar muito na resolução dos exercícios de limites.
1 – O limite da soma é igual à soma dos limites, tal como o limite da diferença é igual à diferença dos limites. Você pode escolher se resolve a soma ou subtração das funções primeiro para depois calcular o limite, ou se calcula o limite de cada função para depois somar ou subtrair os resultados.
![]()
2 – O limite do produto é igual ao produto dos limites. Dependendo das funções envolvidas, fica melhor resolver o produto das funções para depois calcular o limite, assim como pode ser melhor calcular o limite de cada função para depois efetuar a multiplicação.
![]()
3 – O limite do quociente é o quociente dos limites. Lembrando que o denominador tem que ser diferente de zero. A escolha da melhor forma de resolver o exercício fica a seu critério. Você pode resolver a fração das funções e depois calcular o limite do resultado ou calcular o limite de cada função e depois realizar a divisão.
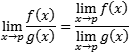
Exercícios resolvidos sobre Limites
1 – Calcule os limites abaixo:
a) O primeiro exercício é bem direto. Dada a função f(x)=(x+2), vamos simplesmente calcular f(1).
![]()
b) O segundo exercício basta calcular f(3).
![]()
c) No terceiro exercício não basta calcular f(3), pois o denominador não pode ser zero. Antes de calcular o limite será necessário mexer na função f(x) para que quando aplicarmos f(3) o denominador não fique igual a zero. Veja a solução do exercício.
![]()
d)![]()
e)![]()
f)![]()
g)![]()
