Exercícios sobre soma, subtração e multiplicação. Além disso, tem exercícios de problemas com interpretação de matrizes.
-
Some as matrizes A e B.

-
Determine a soma das matrizes abaixo:
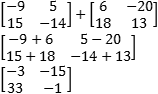
-
Dada as matrizes a seguir, calcule A – B.
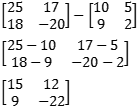
-
Resolva a subtração de matrizes abaixo:

-
Multiplique as matrizes A e B.

-
Determine o produto entre as matrizes abaixo:

-
Calcule a multiplicação das matrizes:
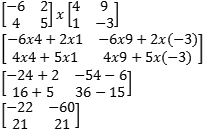
-
Um projeto de pesquisa sobre dietas envolve adultos e crianças de ambos os sexos. A composição dos participantes no projeto é dada pela matriz
 . O número diário de gramas de proteínas, de gorduras e de carboidratos consumidos por cada criança e cada adulto é dado pela matriz
. O número diário de gramas de proteínas, de gorduras e de carboidratos consumidos por cada criança e cada adulto é dado pela matriz  .
.
A partir dessas informações, julgue os itens.
( ) 6000 g de proteínas são consumidos diariamente por adultos e crianças do sexo masculino.
( ) A quantidade de gorduras consumida diariamente por adultos e crianças do sexo masculino é 50% menor que a consumida por adultos e crianças do sexo feminino.
( ) As pessoas envolvidas no projeto consomem diariamente um total de 13200 g de carboidratos.[em breve]
-
O sistema obtido da equação matricial
 é:
é:
a) Possível e indeterminado.
b) Impossível.
c) Possível e determinado com solução (2, 1, –1).
d) Possível e determinado com solução (1, 1, 2).
e) Possível e determinado com solução (– 1, 1, 2).[em breve]
-
Considere o sistema S dado abaixo no julgamento dos itens seguintes.

( ) Se (2; 1; –3) é uma solução do sistema, então k = 2.
( ) O determinante da matriz dos coeficientes do sistema é igual a –3k – 6, portanto k = –2.
( ) Existe um único valor de k para o qual o sistema não possui uma única solução.
() É possível escolher convenientemente o valor de k, de modo que S tenha pelo menos duas soluções distintas.
( ) Se k = –2, a única solução do sistema é a chamada solução trivial (0; 0; 0).[em breve]
Mais exercícios:
