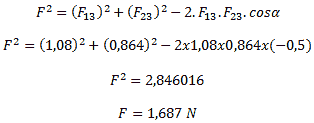Em complemento ao artigo que escrevi sobre força elétrica, disponibilizo aqui alguns exercícios.
1-Calcule a força de atração de duas cargas elétricas Q1 = -2×10-6 C e Q2 = 7×10-5 C no vácuo, sabendo que a constante elétrica do vácuo é de 9×109 N m2/C2 e que a distância entre essas cargas é de 1 metro?
2-Calcule a força de atração entre duas cargas elétricas Q1 = -5×10-6 C e Q2 = 8×10-7 C no vácuo, sabendo que a constante elétrica do vácuo é de 9×109 N m2/C2 e que a distância entre essas cargas é de 0,8 metro?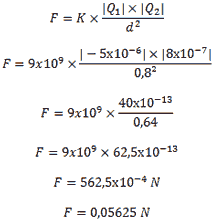
3-Calcule a força de atração de duas cargas elétricas Q1 = 0,5×10-5 C e Q2 = -4×10-6 C no vácuo, sabendo que a constante elétrica do vácuo é de 9×109 N m2/C2 e que a distância entre essas cargas é de 1,3 metro?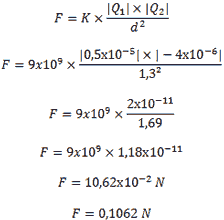
4-Calcule a força de repulsão de duas cargas elétricas Q1 = -2×10-5 C e Q2 = -5×10-5 C no vácuo, sabendo que a constante elétrica do vácuo é de 9×109 N m2/C2 e que a distância entre essas cargas é de 1,5 metro?
5-Calcule a força de repulsão de duas cargas elétricas Q1 = -6×10-6 C e Q2 = -6×10-6 C no vácuo, sabendo que a constante elétrica do vácuo é de 9×109 N m2/C2 e que a distância entre essas cargas é de 0,7 metro?
6-Calcule a força de repulsão de duas cargas elétricas Q1 = 2,2×10-7 C e Q2 = 4×10-5 C no vácuo, sabendo que a constante elétrica do vácuo é de 9×109 N m2/C2 e que a distância entre essas cargas é de 0,5 metro?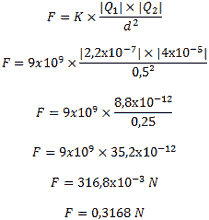
7-Três partículas com cargas Q1 = +5×10-6, Q2 = -4×10-6 e Q3 = +6×10-6 são colocadas sobre um triângulo equilátero de lado d=50 cm, conforme figura abaixo. Calcule a força resultante em Q3.
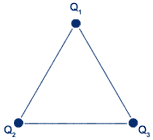
Para calcular a força resultante em Q3, primeiro vamos calcular a força entre (Q1 e Q3) e (Q2 e Q3).
Força de Q1 em Q3, como as cargas são de mesmo sinal, a reação é de repulsão:
Força de Q2 em Q3, como as cargas são de sinais opostos, a reação é de atração:
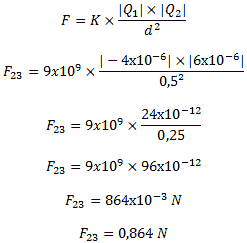
Conforme figura abaixo, vemos que a força resultante é a soma vetorial das forças F12 e F23.
Na figura, o ângulo formado , pois é complemento do ângulo de formado dentro do triangulo. A partir daqui é uma questão de geometria:
