Equação do 2º grau – Exercícios Resolvidos

Sendo que, os coeficientes pertencem ao conjunto dos números reais, mas o coeficiente que acompanha a incógnita quadrática (x²) deve ser diferente de 0.

Como calcular equação do 2º grau

Para resolver exercícios de equação do 2º grau, vamos utilizar a fórmula de Bhaskara.

Devido ao sinal “mais ou menos” entre “b” e a raiz quadrada, vamos obter dois resultados.

Como calcular delta

A parte de que vai dentro da raiz quadrada é chamada de delta.

Portanto, é comum encontrar fórmula de Bhaskara na seguinte forma:

O valor de delta nos indica algumas situações:
• delta for menor que zero, significa que não existe raízes reais para a equação, visto que raiz quadrada de números negativos entra em números complexos, que não pertencem ao conjunto dos números reais.
• delta for igual a zero, então as duas raízes da equação serão iguais.
• delta for maior que zero, a equação possui duas raízes reais diferentes.

Exercícios Resolvidos

1 –Calcule as raízes da equação:

Primeiro vamos identificar os valores dos coeficientes:

Utilizando a fórmula de Bhaskara, temos:

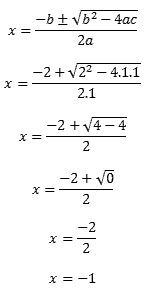
Nesse exercício, as duas raízes da equação de 2º grau são iguais. x1 = x2 = -1
2 – Resolva a equação abaixo:

Vamos identificar os coeficientes:

Aplicando a fórmula de Bhaskara:

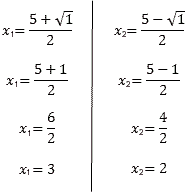
Então, x1 = 3 e x2 = 2.

Basta identificar os coeficientes e substituir na fórmula de Bhaskara. Não tem segredo!