FÓRMULAS DA ACELERAÇÃO
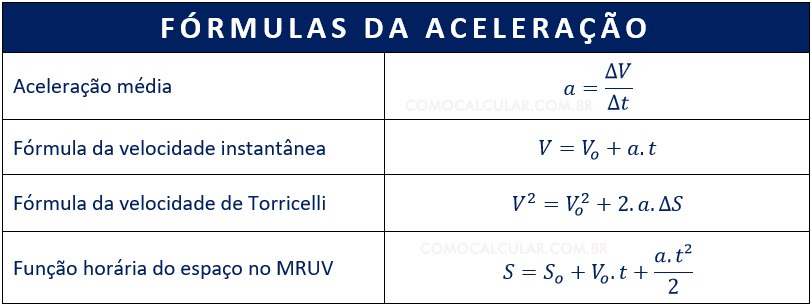
Além da fórmula da aceleração média, que é dada pela razão da variação da velocidade pela variação do tempo, existem outras fórmulas que podem ser utilizadas para calcular a aceleração.
EXERCÍCIOS SOBRE ACELERAÇÃO
01 – Um automóvel percorrendo uma estrada a 90 km/h é freado e para em 5s. A aceleração média introduzida pelos freios, em módulo e em m/s² é:
a) 1
b) 2
c) 4
d) 5
e) 10
02 – Um jovem, partindo do repouso, acelera em linha reta sua moto a 2,5m/s² . Após 4s, a distância percorrida e a velocidade do conjunto é de:
a) 2m e 8m/s
b) 5m e 10m/s
c) 6,5m e 5m/s
d) 20m e 10m/s
e) 40m e 20m/s
03 – Um veículo parte do repouso em movimento retilíneo e acelera com aceleração escalar constante e igual a 2,0m/s² . Pode-se dizer que sua velocidade escalar e a distância percorrida após 3,0 segundos, valem, respectivamente:
a) 6,0 m/s e 9,0m;
b) 6,0m/s e 18m;
c) 3,0 m/s e 12m;
d) 12 m/s e 35m;
e) 2,0m/s e 12m
04 – Dois móveis A e B movimentam-se ao longo de uma trajetória , obedecendo às equações móvel A: SA = 100 + 5,0t e móvel B: SB = 5,0t², onde SA e SB são medidos em m e t em s. Pode-se afirmar que:
a) A e B possuem a mesma velocidade;
b) A e B possuem a mesma aceleração;
c) o movimento de B é uniforme e o de A é acelerado;
d) entre t = 0 e t = 2,0s ambos percorrem a mesma distância;
e) a aceleração de A é nula e a de B tem intensidade igual a 10m/s² .
05 – Um móvel parte do repouso com aceleração constante de intensidade igual a 2,0m/s² em uma trajetória retilínea. Após 20s, começa a frear uniformemente até parar a 500m do ponto de partida. Em valor absoluto, a aceleração de freada foi:
a) 8,0m/s²
b) 6,0m/s²
c) 4,0m/s²
d) 2,0m/s²
e) 1,6m/s²
06 – Uma motocicleta pode manter uma aceleração constante de intensidade 10m/s² . A velocidade inicial de um motociclista, com esta motocicleta, que deseja percorrer uma distância de 500m, em linha reta, chegando ao final desta com uma velocidade de intensidade 100m/s é:
a) zero
b) 5,0m/s
c) 10m/s
d) 15m/s
e) 20m/s
07 – Um automóvel a 108Km/h aciona os freios e para após percorrer 60m. Considerando a aceleração escalar constante, determine o seu valor em m/s² .
a) -7,5
b) 7,5
c) 4,0
d) -4,0
08 – Uma bala perdida, a 350m/s, atinge uma árvore e nela penetra a uma distância de 12cm antes de parar. Pode-se afirmar que, aproximadamente:
a) a aceleração da bala, em módulo, é de 5104,2m/s² .
b) a aceleração da bala, em módulo, é de 51041m/s² .
c) a aceleração da bala, em módulo, é de 51 x 103km/s² .
d) a bala leva 0,0685s para parar.
e) a bala leva 0,685 mile segundos para parar.
09 – Partindo do repouso, um avião percorre a pista, com aceleração constante, e atinge a velocidade de 360 Km/h, em 25 segundos. Qual o valor da aceleração em m/s-2?
a) 9,8
b) 7,2
c) 6,0
d) 4,0
e) 5,5
10 – Partindo do repouso, um avião percorre a pista de decolagem com aceleração constante e atinge a velocidade de 360 km/h em 25s. Qual o valor da aceleração em m/s²?
11 – Um carro está viajando numa estrada retilínea com a velocidade de 72 km/h. Vendo adiante um congestionamento no trânsito, o motorista aplica os freios durante 2,5s e reduz a velocidade para 54 km/h. Supondo que a aceleração é constante durante o período de aplicação dos freios, calcule o seu módulo, em m/s².
a) 1,0
b) 1,5
c) 2,0
d) 2,5
e) 3,0
12 – Um automóvel trafega com velocidade constante de 12 m/s por uma avenida e se aproxima de um cruzamento onde há um semáforo com fiscalização eletrônica. Quando o automóvel se encontra a uma distância de 30 m do cruzamento, o sinal muda de verde para amarelo. O motorista deve decidir entre parar o carro antes de chegar ao cruzamento ou acelerar o carro e passar pelo cruzamento antes de o sinal mudar para vermelho. Este sinal permanece amarelo por 2,2s. O tempo de reação do motorista (tempo decorrido entre o momento em que o motorista vê a mudança de sinal e o momento em que realiza alguma ação) é 0,5s.
a) Determine a mínima aceleração constante que o carro deve ter para parar antes de atingir o cruzamento e não ser multado.
b) Calcule a menor aceleração constante que o carro deve ter para passar pelo cruzamento sem ser multado. Aproxime (1,7)²=3,0
13 – Uma equipe de resgate se encontra num helicóptero, parado em relação ao solo a 305 m de altura. Um paraquedista abandona o helicóptero e cai livremente durante 1,0s, quando abre-se o paraquedas. A partir desse instante, mantendo constante seu vetor velocidade, o paraquedista atingirá o solo em (Dado: g = 10 m/s².):
a) 7,8s.
b) 15,6s.
c) 28s.
d) 30s.
e) 60s.
14 – Um jogador de basquetebol consegue dar um grande impulso ao saltar e seus pés atingem a altura de 1,25 m. A aceleração da gravidade no local tem o valor de 10 m/s². O tempo que o jogador fica no ar, aproximadamente, é:
a) 1s.
b) 2s.
c) 3s.
d) 4s.
e) 5s.
15 – No instante t = 0s, um corpo de massa 1 kg é largado, a partir do repouso, 80 m acima da superfície terrestre. Considere desprezíveis as forças de resistência do ar. Para esse movimento, são feitas três afirmativas:
I) No instante t = 3s, a velocidade do corpo é 30 m/s e está dirigida para baixo.
II) Considerando a origem no solo, a equação horária do movimento é h = 80 – 5t².
III) No instante t = 2s, a aceleração do movimento vale 20 m/s².
Quais afirmativas estão corretas?
a) Apenas II.
b) Apenas III.
c) Apenas I e II.
d) Apenas I e III.
e) I, II e III.
16 – Do alto de uma ponte, a 20 m de altura sobre um rio, deixa-se cair uma laranja, a partir do repouso. A laranja cai dentro de uma canoa que desce o rio com velocidade constante de 3,0 m/s. No instante em que a laranja inicia a queda, a canoa deve estar a uma distância máxima da vertical da queda, em metros, igual a (Dado: g = 10 m/s².):
a) 9,0.
b) 6,0.
c) 4,5.
d) 3,0.
e) 1,5.
17 – A lâmpada do teto de um elevador se desprende quando este sobe com velocidade constante de 2,50 m/s. Sabendo que a lâmpada atinge o piso do elevador em 0,70s, a distância entre o teto e o piso é de: (Adote g = 10 m/s².)
a) 1,90 m.
b) 2,00 m.
c) 2,25 m.
d) 2,45 m.
e) 2,50 m.
GABARITO
1 – d
2 – d
3 – a
4 – e
5 – a
6 – a
7 – b
8 – e
9 – d
10 – 4m/s²
11 – c
12 – a)-3m/s² b)2,4m/s²
13 – 30s
14 – a
15 – c
16 – b
17 – d