Área do triângulo

O triângulo é uma das figuras geométricas mais comuns, importantes e utilizadas. Por esta razão, seu estudo é tão cobrado nas provas, inclusive de concursos públicos. Imaginem um marceneiro que não sabe calcular a área de um simples triângulo. Em apartamentos, principalmente, que são menores a noção de espaço é fundamental.
Podemos dizer que existe três tipos de triângulos: equiláteros, isósceles e escalenos.

• Equiláteros: as medidas de todos os lados são iguais (congruentes), consequentemente todos os ângulos internos medem 60°. Por essa característica, o triângulo equilátero é classificado como triângulo acutângulo ou ainda triângulo equiângulo.
• Isósceles: as medidas de dois lados são iguais e um lado é diferente, consequentemente dois ângulos internos são congruentes. Os ângulos que são congruentes são os que fazem ângulo nas extremidades do lado de medida diferente.
• Escalenos: as medidas de todos os lados são diferentes, consequentemente todos os ângulos internos são distintos.

Condição de existência do triângulo

Quando estudamos triângulos, o professor nos ensina que, para que seja possível formar um triângulo qualquer dos lados tem que medir menos que a soma dos outros dois lados e medir mais que o módulo da diferença dos demais lados.
|b-c| < a < b+c
Difícil imaginar? Veja o exemplo:
1-É possível formar um triângulo com três barras de ferro medindo 5 cm, 2 cm e 8cm?
a = 5, b = 2; c = 8
|2-8| < 5 < 2+8

Como podemos ver, não é possível formar um triângulo com essas barras de ferro, pois não satisfaz as condições.
2- É possível formar um triângulo com três barras de ferro medindo 12 cm, 4 cm e 7cm?
a = 12, b = 4; c = 7
|4-7| < 12 < 4+7
Nessa nova situação, também não foi possível formar um triângulo, visto que não satisfez as condições de existência dos triângulos.

Como calcular área do triângulo

A maneira mais simples de visualizar a área do triângulo é dividindo um retângulo na diagonal. Ao fazermos isso obtemos dois triângulos retângulos de mesma área. Veja a figura abaixo:

Sabendo que a área do retângulo é o produto da base pela altura, então quando cortamos o retângulo na diagonal estamos dividindo-o em dois. A partir disso concluímos que a área do triângulo é o produto da base pela altura, dividido por dois.

Nesse caso, temos que saber as medidas da base e altura.

Área do triângulo equilátero

Considere um triângulo equilátero de lado L e altura h. De regra geral, a área é o produto da base pela altura dividido por dois, mas quando se trata do triângulo equilátero pode-se calcular a área sem a medida da altura, basta saber a medida do lado.
Vamos colocar a altura em função do lado utilizando Pitágoras.

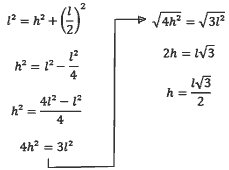
Exercício área do triângulo

1-Calcule a área do triângulo abaixo.

Por se tratar de um triângulo equilátero, podemos utilizar a fórmula da área do triângulo equilátero em função do lado.